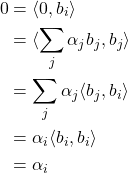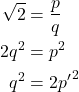A short rant on bad proofs.
Recently I came across a proof concerning orthonormal basis of the following theorem (don’t worry if you know nothing about it):
Theorem. Let 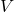 be a vector space with inner (dot) product
be a vector space with inner (dot) product 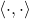 . Let
. Let 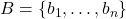 be an orthonormal set of vectors, i.e. the vectors are pairwise orthogonal of norm
be an orthonormal set of vectors, i.e. the vectors are pairwise orthogonal of norm 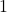 . Then this set is linearly independent.
. Then this set is linearly independent.
The proof I read goes as follows:
Proof Assume by contradiction, that 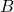 is not linearly independent. This means that there is a non-zero solution
is not linearly independent. This means that there is a non-zero solution 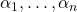 to the equation
to the equation
![Rendered by QuickLaTeX.com \[\sum_{i} \alpha_i b_i = 0\]](https://www.framal.xyz/wp-content/ql-cache/quicklatex.com-7520f22220f3f1451b1ff5181c1d0627_l3.png)
. However, this means that for every
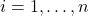
we have
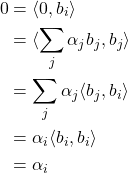
However, we assumed that
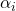
are non-zero, but we just showed that they must be zero. This is a contradiction with our assumption, hence the assumption is wrong, so
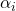
must be zero.

You can read the original proof here, it’s the same, but with more details on why the equalities here hold, which this is irrelevant for this post.
You might already see that something is odd here, especially given the title of this post. How is this exactly a proof by contradiction? Well, in the end we got a contradiction with the assumptions, so technically it is proof by contradiction. However, it is practically a very direct proof. Where did we use the assumption? It wasn’t useful by any means. We had some statement 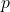 that we wanted to prove, so we assumed
that we wanted to prove, so we assumed 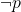 , then showed that
, then showed that 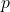 holds, and then concluded that it cannot be that
holds, and then concluded that it cannot be that 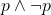 , hence
, hence 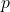 . It’s quite a mental gymnastics here, don’t you agree?
. It’s quite a mental gymnastics here, don’t you agree?
This example may seem artificial, but you can clearly see that I didn’t come up with it on my own. I claim that this pattern can be seen often in the wild, especially when students are presenting proofs on the tutorials.
Example of a good proof by contradiction
A very well known and simple example is the proof that 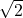 is irrational. In other words, the theorem states that there are no integers
is irrational. In other words, the theorem states that there are no integers 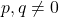 such
such 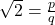 .
.
Proof. Assume by contradiction that there are integers 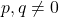 such that
such that 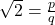 . We may assume without loss of generality, that
. We may assume without loss of generality, that 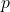 and
and 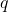 are coprime. Then we have a sequence of equivalent equalities:
are coprime. Then we have a sequence of equivalent equalities:
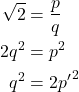
where p’ is
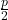
. This is an integer as well, by the
Euclid’s lemma. So, by the same lemma we get that
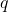
must be divisible by
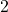
, which is a contradiction with our assumption, that
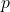
and
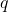
are coprime.

Notice that in this proof we’re actually leveraging the assumption, which wasn’t the case in the former theorem.
What is a proof by contradiction?
Disclaimer. This section is very technical and formal. This may be hideous to some readers. If you despise formal logic and hate Bourbakists, then skip this section for your own sake. I try to formalize what is a proof and why we actually can do a proof by contradiction.
Let’s first establish what is a proof. I don’t want to get in to much details, as this isn’t particularly engaging topic (check out my notes from Logic R if you are interested in a very formal and technical definition). In our case, we can think of a proof of a statement 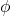 with assumptions
with assumptions 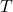 as a sequence of sentences
as a sequence of sentences 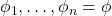 , where a sentence must be an assumption from
, where a sentence must be an assumption from 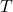 , a tautology, or be concluded directly from some previous statements in the proof. If there exists a proof of
, a tautology, or be concluded directly from some previous statements in the proof. If there exists a proof of 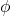 assuming
assuming 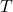 , then we say that
, then we say that 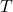 proves
proves 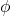 , which is often written as
, which is often written as 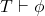 .
.
A proof by contradiction is an approach of proving rather than a technical term. I’ll try to formalize this with so called deduction theorem. It states that if we show that 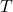 proves
proves 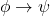 , then
, then 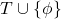 proves
proves 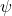 and vice versa. This is again a technical theorem to formalize the fact that if we want to prove an implication A implies B we may simply assume A and then prove that B must hold.
and vice versa. This is again a technical theorem to formalize the fact that if we want to prove an implication A implies B we may simply assume A and then prove that B must hold.
Let’s say we want to prove some theorem 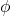 . To show that
. To show that 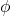 is true, we could show that the following implication is true:
is true, we could show that the following implication is true: 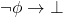 (where
(where 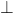 is basically false, you could interpret it as a sentence
is basically false, you could interpret it as a sentence 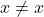 , which is always false). We could do that as
, which is always false). We could do that as 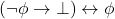 . So, every proof by contradiction has the following scheme: First prove that
. So, every proof by contradiction has the following scheme: First prove that 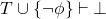 , by deduction theorem
, by deduction theorem 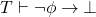 . Thanks to modus ponens we can then extend the proof of this implication and finally show that
. Thanks to modus ponens we can then extend the proof of this implication and finally show that 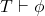 .
.
Conclusions
I like tidy and deliberate proofs. I also like when a presenter of a solution to some problem on the blackboard gives the viewers a nice and enjoyable experience. This post provides an example of one of the common shortcomings in presenting proofs. It’s not faulty reasoning, but it’s unnecessary and could be simplified and organized at a low cost. I try to pay attention to the preciseness and cleanliness of my solutions. If you ever see me presenting and saying something in a bad fashion, then please don’t mind telling me that!