[Pl/En] Piękne zadanie z zimowych warsztatów informatycznych (Wonderful task from winter programming workshops)

English version of this site is on the bottom of this page.

Kto by pomyślał, że są uczniowie szkół podstawowych, którzy chcieliby poświęcić 5 dni swoich ferii zimowych na naukę programowania i algorytmiki. A jednak, w dniach 3-5 oraz 11-12 lutego przeprowadziłem warsztaty algorytmiczne, które odbyły się w budynku XIV liceum ogólnokształcącego we Wrocławiu. Ku mojemu zadowoleniu, na wszystkich warsztatach pojawiało się stacjonarnie mniej więcej 20 osób, a do tego kilka brało udział w zajęciach zdalnie.

Wszystkie warsztaty odbywały się z tą samą formułą. O godzinie 9:30 rozpoczynał się contest (tak zwykle mówimy na zawody algorytmiczne w świecie programowania sportowego), który trwał 4 godziny. W trakcie zawodów uczniowie mieli do pokonania 3 zadania, w każdym do zdobycia od 0 do 100 punktów. Zawody miały imitować II etap Olimpiady Informatycznej Juniorów, w której niebawem weźmie udział większość uczniów biorących udział w warsztatach. Po zakończeniu contestu i krótkiej przerwie przechodziliśmy do dyskusji i omówienia każdego z zadań, a następnie do krótkiego, dodatkowego wykładu.

Jeszcze raz chciałbym podkreślić, że wszyscy uczniowie przyszli na zajęcia z własnej woli, w trakcie ferii zimowych, w swoim czasie wolnym, który postanowili przeznaczyć na naukę programowania. Wydaje mi się, że jest to znakomity przykład, że nauka przedmiotów ścisłych nie musi kojarzyć się z udręką i obowiązkiem, a zabawą i satysfakcjonującym spędzaniem czasu.

Wszystkie zadania, które pojawiły się w trakcie warsztatów, zostały przygotowane przeze mnie, na podstawie innych zadań z konkursów z poprzednich lat, z różnych konkursów algorytmicznych (np. atcoder.jp czy usaco.org). Zadania są ogólnodostępne na całkowicie darmowej stronie solve.edu.pl, pod zakładką wydarzenia, pod kategorią Warsztaty przygotowujące do II etapu OIJ, ferie 2025. Zachęcam do zapoznania się z nimi i własną próbą rozwiązania.

W tym poście chciałem omówić moje ulubione z zadań, którego rozwiązanie wyjątkowo mi się podoba.

Zadanie Poprawne klockowanie

Treść. Dane są klocki, na których napisane są ciągi nawiasów otwierających i zamykających. Czy da się ułożyć klocki obok siebie tak, żeby otrzymane nawiasowanie było poprawne?

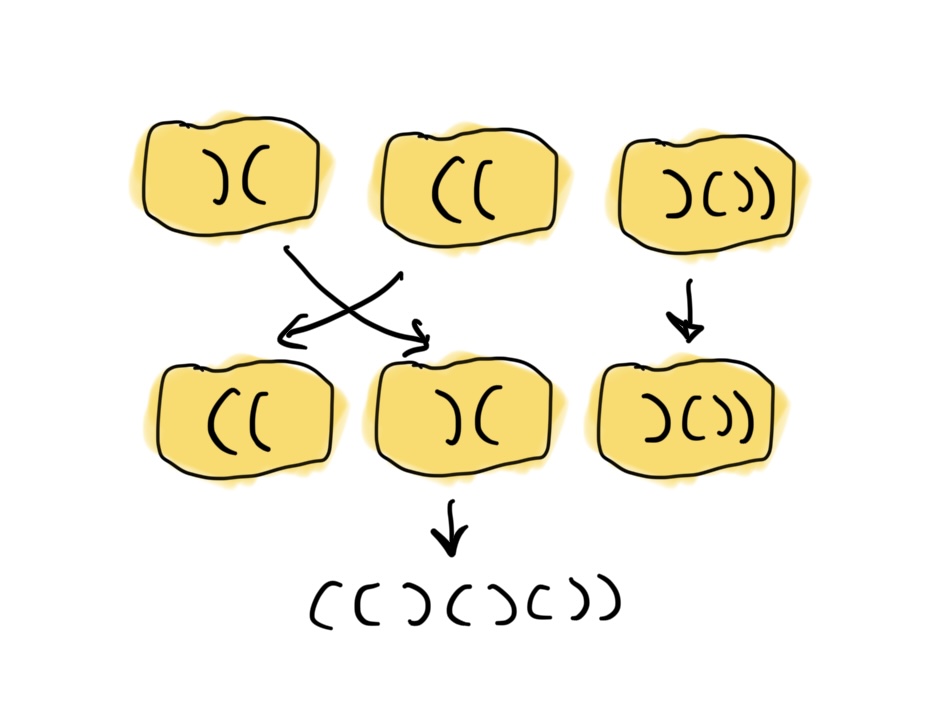
Bardzo lubię historyjki w zadaniach, które pozwalają prosto i trafnie wizualizować rozwiązywany problem. Dokładnie takie jest to zadanie, nawiązujące do klasycznego problemu weryfikacji, czy podany ciąg nawiasów jest “poprawny”. Intuicyjna definicja poprawnego nawiasowania jest prosta – nawiasowanie jest poprawne, jeżeli każdemu nawiasowi otwierającemu możemy przypisać nawias zamykający. Formalna definicja wymaga pewnego formalizmu, który może wydawać się skomplikowany, ale po chwili przemyślenia okazuje się, że bardzo dokładnie przedstawia strukturę poprawnych nawiasowań.

Definicja. Ciąg otwierających i zamykających nawiasów nazywany nawiasowaniem. Zbiór poprawnych nawiasowań definiujemy rekurencyjnie przez poniższe warunki:

1. Ciąg pusty (brak nawiasów) jest poprawnym nawiasowaniem.
2. Jeżeli A jest poprawnym nawiasowaniem, to (A) też jest.
3. Jeżeli A oraz B są poprawnymi nawiasowaniami, to AB również jest poprawnym nawiasowaniem.

Żeby lepiej zrozumieć powyższą definicję, przyjrzyjmy się kilku przykładom.

• Ciąg () jest poprawnym nawiasowaniem. Dlaczego? Ponieważ, wg definicji, brak nawiasów jest poprawnym nawiasowaniem! Jeżeli przyjmiemy, że A oznacza własnie ten pusty ciąg, to wtedy () = (A) . Zatem () jest poprawnym nawiasowaniem.
• Możemy to teraz pociągnąć dalej. Skoro () jest poprawnym nawiasowaniem, to jest nim też (()) oraz ()(), zgodnie z punktami 2. oraz 3.
• Znowu, (())() jest też poprawnym nawiasowaniem, jest nim też ()() sklejone z (), zatem ()()() jest poprawne. Możemy tak “generować” kolejne nawiasowania w nieskończoność.
• Zauważmy, że nawiasowanie )( nie jest oczywiście poprawne i faktycznie, nasza definicja w żaden sposób nie pozwala nam skonstruować takiego nawiasowania.

Ciekawym pobocznym problemem, który daje się rozwiązać za pomocą powyższej definicji, jest odpowiedź na pytanie ile jest poprawnych nawiasowań długości 2n? Odpowiedź można znaleźć tutaj.

Mogłoby się wydawać, że zaproponowana przeze mnie definicja poprawnego nawiasowania pojawiła się “znikąd” i nie widać jasnego połączenia z naszą pierwszą, intuicyjną definicją (tą, że każdy otwarty nawias musi mieć swój odpowiadający zamykający nawias). Spróbujmy zatem w jakiś sposób połączyć oba pomysły.

W tym momencie wprowadzę jedną z moich ulubionych algorytmicznych sztuczek. Mam wrażenie, że wiele osób, gdy widzi to po raz pierwszy, reaguje zachwytem i ogromną satysfakcją, jakby zobaczyli coś wyjątkowo pięknego. Profesor Jerzy Marcinkowski, jeden z moich wykładowców akademickich, porównuje to zjawisko do momentu wejścia na szczyt górski, na którym widać długo wyczekiwaną panoramę, którą nie sposób się nie zachwycać. Jest to kolejny przykład, że w matematyce nieoczekiwane połączenia prowadzą do zaskakujących odkryć i może właśnie dlatego 14-letni uczniowie, w ramach swojej zimowej przerwy, decydują się przychodzić na warsztaty informatyczne.

Pomyślmy, że każdy ciąg nawiasów to tak naprawdę ciąg liczb. Zamieńmy wszystkie nawiasy otwierające na 1, a zamykające na -1. Następnie, idąc po kolei, notujmy aktualną sumę wszystkich napotkanych liczb. Obrazek poniżej prezentuje jak wyglądałby wykres takiego procesu dla przykładowego, poprawnego nawiasowania.

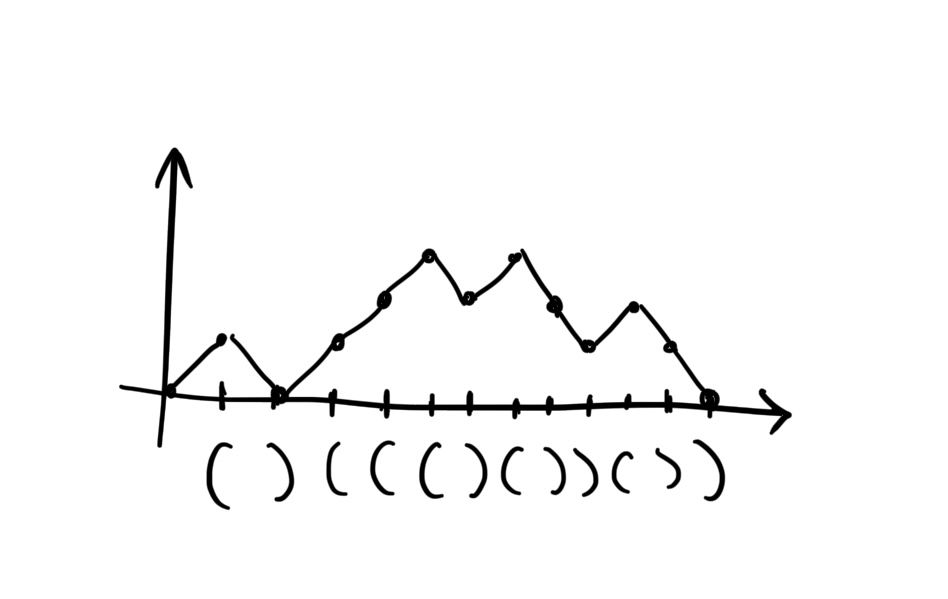
Zauważ, że nie musimy już myśleć o ciągu nawiasowań jak o ciągu znaków. Możemy myśleć jak o wykresie, który co jeden krok “idzie” o 1 stopień w górę lub w dół, ale nigdy nie stoi w miejscu. To działa również w drugą stronę, gdybym narysował taki wykres, to z łatwością jesteś w stanie stwierdzić, jakie nawiasowanie (poprawne czy nie) stoi za tym wykresem. Zanim zaczniesz czytać dalej, spróbuj samodzielnie narysować wykresy tych nawiasowań: ((())), ())(() oraz ((). Które z nich to poprawne nawiasowania? Czym różnią się ich wykresy?

---

Zastanówmy się zatem – jak wyglądają wykresy, które przedstawiają poprawne nawiasowania, wg naszej intuicyjnej definicji?

1. Wykres musi kończyć w 0. Gdyby tak nie było, to znaczyłoby, że liczba jedynek oraz “minus jedynek” nie była taka sama, a to oznacza, że nawiasów otwierających i zamykających również była różna liczba. A przecież każdy nawias otwierający mieliśmy sparować z pewnym nawiasem zamykającym.
2. Gdyby wykres kiedykolwiek spadł poniżej zera, to nie może przedstawiać poprawnego nawiasowania. W pewnym momencie musiała istnieć sytuacja, że nawiasów zamykających było za dużo względem otwierających, zatem nie byłoby możliwości, żeby je sparować.

Sytuację z punktu 1. widać, kiedy rysuje się wykres nawiasowania ((). Sytuację z punktu drugiego obrazuje wykres nawiasowania ())(().

Dobrze, ale co to wszystko ma wspólnego z naszą formalną, rekurencyjną definicją? Okazuje się, że bardzo dużo. Przedstawione punkty to tylko jedynie warunki konieczne, które wykres musi spełniać, żeby przedstawiał poprawne nawiasowanie. Skąd mamy pewność, że nie istnieje pewne nawiasowanie, które spełnia oba punkty, a jest niepoprawne (czy to wg intuicyjnej, czy tej formalnej definicji?). Ostatecznym spoiwem łączącym nasze obie definicje będzie indukcja matematyczna.

Jeżeli nigdy nie słyszeliście o indukcji matematycznej, to się tym nie przejmujcie i spróbujcie na spokojnie przeczytać poniższy dowód. Spróbowałem odpuścić sobie trochę formalizmu w imię łatwiejszego i bardziej przystępnego dowodu, który powinien być intuicyjny dla każdego, kto dotarł do tego miejsca wpisu.

Twierdzenie. Jeżeli wykres nawiasowania kończy się w zerze oraz nigdy nie spada poniżej zera, to to nawiasowanie jest poprawne wg formalnej definicji.

Dowód. Po pierwsze zauważmy, że faktycznie nasze twierdzenie jest prawdziwe dla pustego ciągu nawiasów. Wykres takiego nawiasowania to po prostu “punkt” w przecięciu osi współrzędnych. Zaczyna oraz kończy się w zerze oraz nigdy nie schodzi poniżej zera. Rozważmy teraz jakieś bardziej skomplikowane nawiasowanie, nazwijmy je S. Załóżmy, że wykres tego nawiasowania spełnia oba warunki 1. i 2. Mamy dwa przypadki, przedstawione na rysunku.

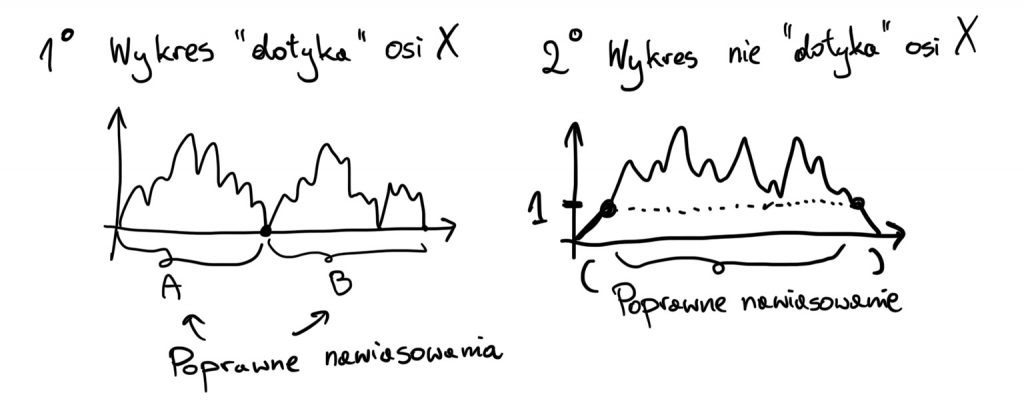
• Przypadek 1. Wykres S “dotyka” zero w pewnym punkcie między początkiem i końcem. To oznacza, że S można podzielić na dwa wykresy, które oba zaczynają się i kończą w zerze, ale przedstawiają krótsze nawiasowania. Co to oznacza? Że S jest sklejeniem dwóch nawiasowań A oraz B, a ich wykresy również spełniają warunki 1. i 2. Możemy zastosować dla nich teraz to samo rozumowanie i okaże się, że oba są poprawnymi nawiasowaniami, a zatem, zgodnie z definicją, S również jest poprawne.
• Przypadek 2. Wykres S nie “dotyka” zera poza początkiem i końcem. Skoro wykres nigdy nie spada poniżej zera, to na początku wykresu musimy iść w górę, a na końcu w dół. Zatem pierwszy i ostatni nawias S to odpowiednio ( oraz ). To świetnie, bo możemy te nawiasy ze sobą sparować, a to co zostanie, to krótsze nawiasowanie, którego wykres również spełnia warunki 1. oraz 2.! Stosując nasze rozumowanie dla tego krótszego nawiasowania okaże się, że S jest postaci (A), gdzie A jest poprawnym nawiasowaniem, zatem jest nim też S.

Tym dowodem połączyliśmy naszą intuicję z formalną definicją, która mówi o tym, jak można “produkowć” poprawne nawiasowania. Dzięki temu wiemy również jak powinien wyglądać algorytm, który sprawdza, czy dany ciąg nawiasów jest poprawny!

funkcja czy_poprawne(nawiasowanie):
  suma = 0
  dla kolejnych nawiasów c z nawiasowania:
    jeżeli c == '(':
      suma = suma + 1
    w przeciwnym wypadku:
      suma = suma - 1
    jeżeli suma < 0
      zwróć false
  zrwóć (suma == 0)

Rozwiązanie zadania.

Wróćmy do naszego pierwotnego zadania, Poprawne klockowanie. Skoro wiemy już jak sprawdzać, czy dany ciąg nawiasów jest poprawny, spróbujmy przenieść to do naszego problemu. Zgodnie z naszą interpretacją, każdy z klocków będzie tworzył pewną część wykresu.

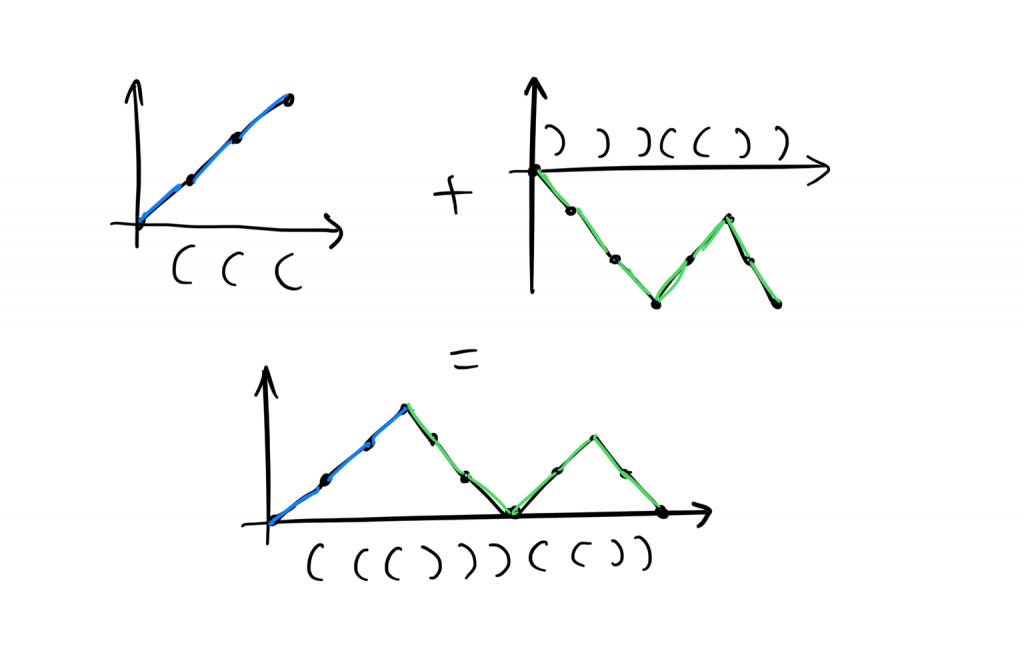
Z osobna, żaden z wykresów nie przedstawia poprawnego nawiasowania. Jednak sklejenie ich ze sobą w odpowiedniej kolejności powoduje, że powstały wykres spełnia wszystkie warunki konieczne, żeby reprezentować poprawne nawiasowanie. Zadanie zatem zupełnie się zmieniło. Teraz nie myślimy już o układaniu nawiasowań, a o układaniu wykresów i sklejaniu ich ze sobą końcami tak, żeby końcowy wykres zaczynał i kończył się w zerze, a ponadto nigdy nie spadł poniżej zera.

Nie interesuje nas zatem jak dokładnie ten wykres mógłby wyglądać. Rozważając konkretny klocek interesuje nas jedynie to, na jakiej wartości się kończy oraz jak bardzo spada poniżej zera. Każdy klocek zmienia się w parę liczb: końcową wartość wykresu oraz jak bardzo spadł poniżej zera w pewnym momencie. Dla przykładu, klocek (() dałby parę liczb (1, 0), klocek ))(((( parę (2, -2), a klocek ()))( parę (-1 , -2).

Jeżeli miałaby istnieć jakaś kolejność klocków, która utworzy poprawne nawiasowanie, to jak mogłaby ona wyglądać? Intuicja podpowiada, że na początku warto ustawiać klocki, których wykres kończy się powyżej zera. Dzięki temu będziemy mieć maksymalny “zapas”, na wypadek, gdyby trafił się klocek, którego wykres spada diametralnie poniżej zera. Ponadto, najpierw bardziej opłaca ustawiać się klocki, których minimalna wartość jest jak największa. Przykładowo klocek )))(((((( mimo tego, że koniec końców kończy na wysokości 3, to nie może zostać postawiony na początku. Lepiej byłoby ustawić np. klocki (, a potem )((((. Zatem, pierwsza faza algorytmu, którą nazwiemy fazą dodatnią, wygląda następująco:

Faza dodatnia. Posortuj klocki, których wykresy kończą się ponad zerem lub w zerze, malejąco względem ich minimalnego punktu.

Biorąc nawiasowania zaproponowane powyżej, ich pary wyglądałyby następująco: (3, -3), (1, 0) oraz (3, -1). Wtedy, posortowanie malejąco wg minimalnej wartości, da nam kolejność (1, 0), (3, -1), (3, -3). (Zauważ, że liczby ujemne maleją “na odwrót”, tzn. -3 jest mniejsze niż -1 czy 0).

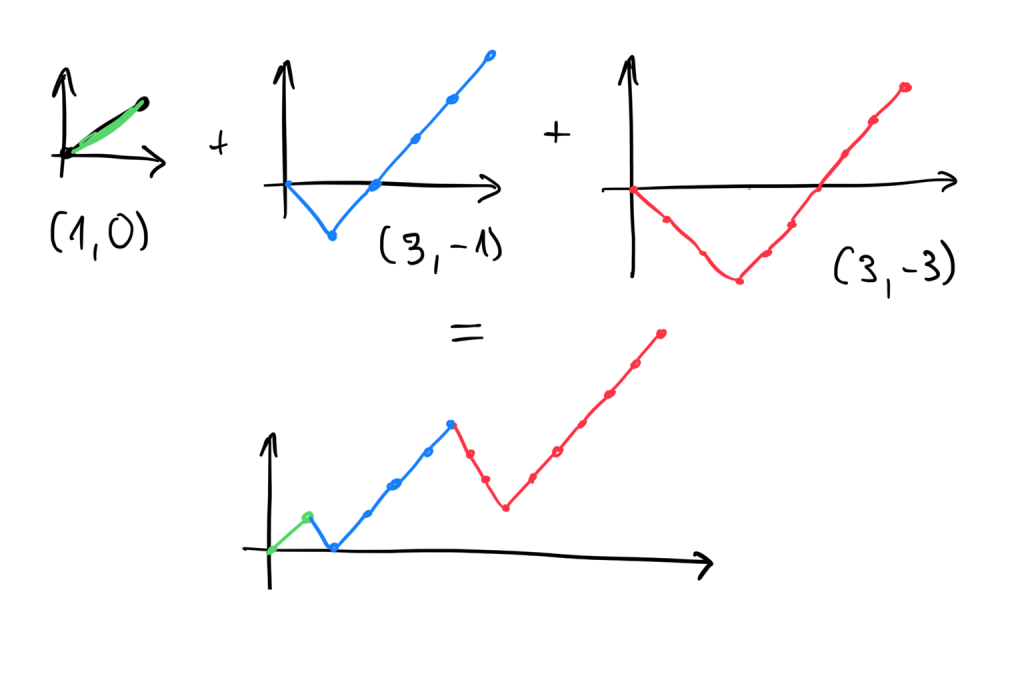
Jeżeli taka kolejność nie zapewni, że wykres jest zawsze powyżej zera, to możemy śmiało stwierdzić, że żadna inna też tego nie zapewnia. Dokładny dowód, że faktycznie tak jest, pozostawiam dla czytelnika do samodzielnego przemyślenia (zadaj sobie pytania: co by się stało, gdyby jakiś klocek, który spada poniżej zera o 10, ustawił przed klockiem, który spada poniżej zera o 5? Czy mogę coś z tego zyskać? Czy mógłbym coś stracić, gdybym ustawił je w odwrotnej kolejności?).

Jak w takim razie poradzić sobie z kolejnością klocków, których wykresy kończą się poniżej zera? Intuicja podpowiada, że najpierw chcemy ustawiać klocki, których minimum jest jak największe, ponieważ mamy największy zapas dzięki klockom, które “podnosiły” koniec wykresu. Czy możemy zatem posortować je wg rosnącego minimum? Odpowiedź to… tak i nie. Rozważmy następujący przykład z trzema klockami ((((, ))) i ))(. Ich odpowiadające pary to kolejno (4, 0), (-3, -3) oraz (-2, -1). Gdybyśmy posortowali klocki, które kończą się poniżej zera rosnąco po minimach, to otrzymalibyśmy nawiasowanie (((()))))(, które oczywiście nie jest poprawne, natomiast nawiasowanie (((())())) już jest.

W tym miejscu zastosujemy kolejny piękny trick, dzięki któremu rozwiązanie staje się tak samo proste, jak w przypadku klocków z dodatnim końcem. Zauważmy, że gdyby klocki, których wykresy kończą się poniżej zera, czytać od tyłu, to nagle staną się klockami, których wykresy kończą się powyżej zera. A przecież takie klocki już umiemy uporządkować!

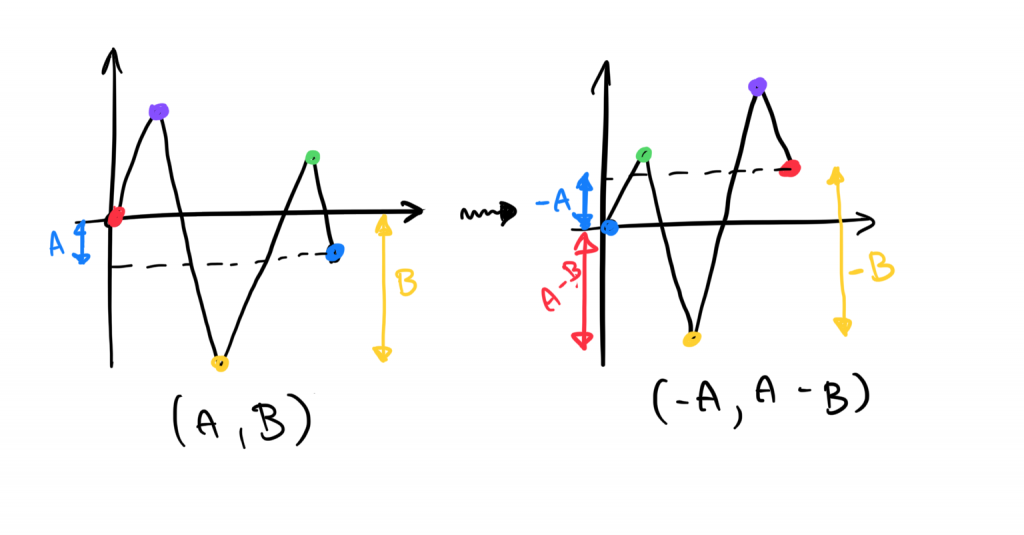
Jeżeli dany wykres kończy się na wysokości A (zauważ, że A jest ujemne), to odbity wykres skończy się na wysokości -A. Ponadto, zmieni się jego minimalna wartość. Na powyższym obrazku łatwo zauważyć, że nasza nowa minimalna wartość musi wynosić A-B. Zatem, faza ujemna algorytmu działa następująco.

Faza ujemna. Zmień wszystkie pary (A, B) w pary (-A, A-B) i uruchom na nich fazę dodatnią.

Cały algorytm ma zatem następującą postać:

1. Sprawdź, czy nawiasów otwierających jest tyle samo, co nawiasów zamykających na wszystkich klockach. Jeżeli nie, to od razu zakończ niepowodzeniem.
2. Zmień wszystkie klocki w ich odpowiadające pary (końcowa wartość wykresu, minimalna wartość wykresu).
3. Posegreguj klocki w dwie listy, jedną z nieujemnymi końcami, drugą z ujemnymi.
4. Uruchom pierwszą fazę na nieujemnych klockach. Jeżeli taka kolejność tworzy wykres, który spada poniżej zera, zakończ niepowodzeniem.
5. Uruchom drugą fazę na ujemnych klockach. Jeżeli taka kolejność tworzy wykres, który nie spada poniżej zera, zakończ sukcesem.

Rozwiązanie nie wydaje się hardcorowe, jednak żadnemu uczestnikowi nie udało się rozwiązać go w trakcie zawodów. Uczestnicy wrzucali bardzo dużo rozwiązań, które na pierwszy rzut oka wydawały się poprawne, jednakże po analizie ich kodów udawało mi się znajdować takie przykłady klocków, które pokazywały, że ich algorytm nie działa poprawnie. Okazywało się, że to właśnie druga faza sprawiła im najwięcej kłopotów. W ich obronie muszę powiedzieć, że w pierwszym podejściu do tego zadania popełniałem ten sam błąd i dopiero po chwili przemyślenia byłem w stanie zrozumieć jak sprytnie można uporać się z drugą częścią klocków.

Dla wszystkich zainteresowanych, serdecznie zapraszam do samodzielnej próby rozwiązania zadania. Poprawność rozwiązania można sprawdzić tutaj.

Bardzo dziękuję za doczytanie do końca! Jeżeli spodobał Ci się ten wpis, masz jakieś pytania lub uwagi, serdecznie zachęcam do zostawienia komentarza albo skontaktowania się ze mną bezpośrednio na mojego maila. Do zobaczenia w następnym wpisie 🙂

---

Who would have thought that there are primary school students who would want to spend 5 days of their winter break learning programming and algorithms. However, on February 3-5 and 11-12, I conducted algorithmic workshops that took place in the building of the XIV High School in Wrocław. To my satisfaction, approximately 20 people attended all workshops in person, and several more participated remotely.

All workshops followed the same format. At 9:30, a contest (as we usually call algorithmic competitions in the competitive programming world) began, lasting 4 hours. During the competition, students had to solve 3 problems, with 0 to 100 points available for each. The aim was to imitate the second stage of the Junior Olympiad in Informatics, which most of the workshop participants will soon take part in. After the contest and a short break, we moved on to discussion and review of each problem, followed by a brief, additional lecture.

I would like to emphasize again that all students came to the classes voluntarily, during winter break, in their free time, which they chose to dedicate to learning programming. I think this is an excellent example that learning STEM subjects doesn’t have to be associated with torment and obligation in young people’s minds, but rather with fun and satisfying time spent.

All problems that appeared during the workshops were prepared by me, based on other problems from previous years’ competitions from various algorithmic contests (e.g., atcoder.jp or usaco.org). The problems are publicly available on the completely free website solve.edu.pl, under the events tab, under the category Workshops preparing for OIJ Stage II, Winter 2025. I encourage you to check them out and try solving them yourself (unfortunately, most of the task descriptions are written in polish).

In this post, I wanted to discuss my favorite problem, whose solution I particularly like.

Valid Block Arrengament Problem

Description. There are blocks with sequences of opening and closing brackets written on them. Is it possible to arrange the blocks next to each other so that the resulting bracket sequence is valid?

I really like stories in problems that allow for simple and accurate visualization of the problem being solved. This is exactly such a problem, referring to the classic problem of verifying whether a given sequence of brackets is “valid”. The intuitive definition is also simple – a bracket sequence is valid if we can assign a closing bracket to each opening bracket. The formal definition requires some formalism that might seem complicated, but after a moment’s thought, it turns out that it very precisely represents the structure of valid bracket sequences.

Definition: A sequence of opening and closing brackets is called a bracketing. The set of valid bracketings is defined recursively by the following conditions:

1. An empty sequence (no brackets) is a valid bracketing.
2. If A is a valid bracketing, then (A) is also valid.
3. If A and B are valid bracketings, then AB is also a valid bracketing.

To better understand the above definition, let’s look at some examples.

• The sequence () is a valid bracketing. Why? Because, according to the definition, no brackets is a valid bracketing! If we assume that A represents this empty sequence, then () = (A). Therefore () is a valid bracketing.
• We can take this further. Since () is a valid bracketing, (()) and ()() are also valid, according to points 2. and 3.
• Again, (())() is also a valid bracketing, and ()() concatenated with () makes ()()() valid. We can “generate” more bracketings like this indefinitely.
• Note that the bracketing )( is obviously not valid, and indeed, our definition doesn’t allow us to construct such a bracketing in any way.

It might seem that my proposed definition of valid bracketing appeared “out of nowhere” and there’s no clear connection with our first, intuitive definition (the one where each opening bracket must have its corresponding closing bracket). Let’s try to somehow connect both ideas.

At this point, I’ll introduce one of my favorite algorithmic tricks. I feel that when many people see this for the first time, they react with delight and great satisfaction, as if they’ve seen something exceptionally beautiful. Professor Jerzy Marcinkowski, one of my academic lecturers, compares this phenomenon to the moment of reaching a mountain peak where you see a long-awaited panorama that’s impossible not to admire. This is another example of how unexpected connections in mathematics lead to surprising discoveries, and perhaps that’s why 14-year-old students choose to come to IT workshops during their winter break.

Let’s think of each bracket sequence as actually being a sequence of numbers. Let’s replace all opening brackets with 1 and closing brackets with -1. Then, going sequentially, we’ll note the current sum of all encountered numbers. The image below shows what such a process’s graph would look like for an example valid bracketing.

Notice that we no longer need to think about the bracket sequence as a sequence of characters. We can think of it as a graph that “goes” up or down by 1 step every step, but never stays in place. This works in reverse too – if I drew such a graph, you could easily determine what bracketing (valid or not) stands behind this graph. Before reading further, try to draw graphs for these bracketings yourself: ((())), ())(() and ((). Which of them are valid bracketings? How do their graphs differ?

---

So let’s think – what do graphs that represent valid bracketings look like, according to our intuitive definition?

1. The graph must end at 0. If it didn’t, it would mean that the number of 1s and -1s wasn’t the same, which means the number of opening and closing brackets wasn’t equal either. And we were supposed to pair each opening bracket with a closing one.
2. If the graph ever fell below zero, it can’t represent a valid bracketing. At some point, there must have been a situation where there were too many closing brackets relative to opening ones, so it wouldn’t be possible to pair them.

The situation from point 1 can be seen when drawing the graph of bracketing ((). The situation from point two is illustrated by the graph of bracketing ())(().

Good, but what does all this have to do with our formal, recursive definition? It turns out, quite a lot. The presented points are only necessary conditions that a graph must meet to represent a valid bracketing. But how do we know there isn’t some bracketing that meets both points but is invalid (whether according to the intuitive or formal definition)? The final link connecting our two definitions will be mathematical induction.

If you’ve never heard of mathematical induction, don’t worry about it and try to calmly read through the following proof. I tried to let go of some formalism in favor of an easier and more accessible proof that should be intuitive for anyone who has reached this point in the post.

Theorem. If a bracketing’s graph meets conditions 1 and 2 presented above, i.e., ends at zero and never goes below zero, then this bracketing is valid according to the formal definition.

Proof. First, let’s notice that our theorem is indeed true for an empty bracket sequence. The graph of such a bracketing is just a “point” at the intersection of the coordinate axes. It starts and ends at zero and never goes below zero. Now let’s consider some more complicated bracketing, let’s call it S. Assume that this bracketing’s graph meets both conditions 1 and 2. We have two cases, shown in the figure.

• Case 1: S‘s graph “touches” zero at some point between the beginning and end. This means that S can be divided into two graphs, both starting and ending at zero, but representing shorter bracketings. What does this mean? That S is a concatenation of two bracketings A and B, and their graphs also meet conditions 1 and 2. We can now apply the same reasoning to them, and it will turn out that both are valid bracketings, and therefore according to the definition, S is also valid.
• Case 2: S‘s graph doesn’t “touch” zero except at the beginning and end. Since the graph never goes below zero, we must go up at the beginning of the graph and down at the end. Therefore, the first and last brackets of S are ( and ) respectively. That’s great because we can pair these brackets, and what remains is a shorter bracketing whose graph also meets conditions 1 and 2! Applying our reasoning to this shorter bracketing, it turns out that S is of the form (A), where A is a valid bracketing, therefore S is also valid.

With this proof, we connected our intuition with the formal definition that tells us how to “produce” valid bracketings. Thanks to this, we also know how an algorithm that checks whether a given sequence of brackets is valid should look!

function is_valid(bracketing):
  sum = 0
  for each bracket c in bracketing:
    if c == '(':
      sum = sum + 1
    else:
      sum = sum - 1
    if sum < 0
      return false
  return (sum == 0)

Solution to the problem.

Let’s return to our original problem, correct block arrangement. Now that we know how to check if a given bracket sequence is valid, let’s try to transfer this to our problem. According to our interpretation, each block will create a certain part of the graph.

For example, a block that would be placed first must have a bracketing that never goes below zero. But this doesn’t have to be true for the second block. For instance, if the first block had the bracketing (((, then the second could look like this: )))(()).

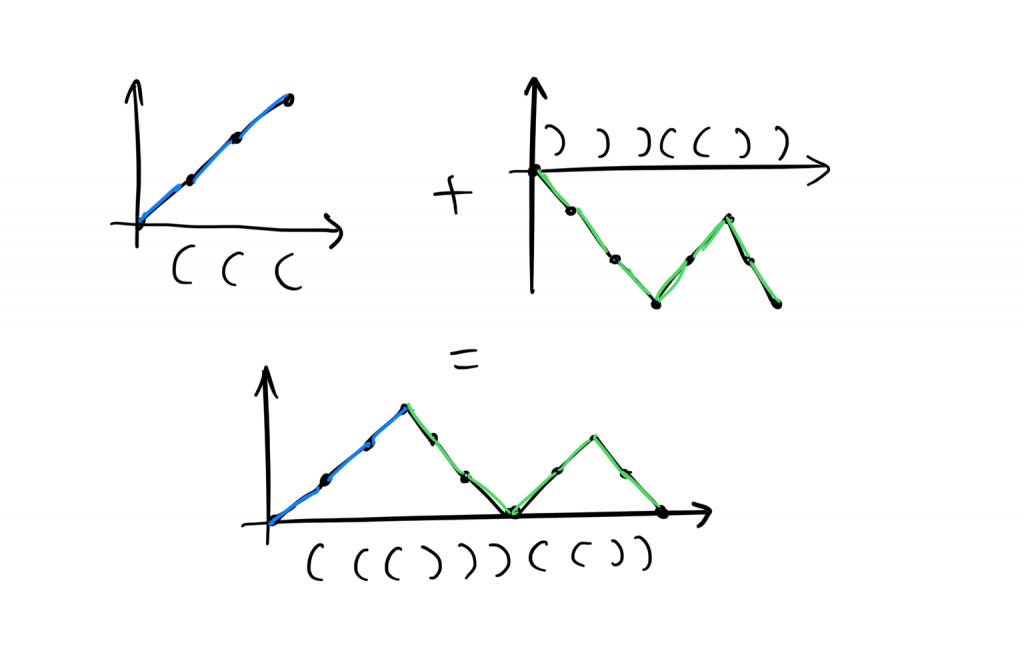
Separately, neither graph is valid. However, joining them together in the right order creates a graph that meets all the necessary conditions to represent a valid bracketing. So the task has completely changed. Now we’re no longer thinking about arranging bracketings, but about arranging graphs and joining their ends together so that the final graph starts and ends at zero, and moreover never falls below zero.

Therefore, we’re not interested in exactly what this graph might look like. When considering a specific block, we’re only interested in what value it ends at and how far below zero it falls. Each block transforms into a pair of numbers: the final value of the graph and how far it fell below zero at some point. For example, the block (() would give the pair of numbers (1, 0), the block ))(((( the pair (2, -2), and the block ()))( the pair (-1, -2).

If there were to be some order of blocks that would create a valid bracketing, what might it look like? Intuition suggests that it’s worth placing blocks whose graph ends above zero at the beginning. This way, we’ll have maximum “reserve” in case we encounter a block whose graph falls dramatically below zero. Moreover, it’s more beneficial to first place blocks whose minimum value is as high as possible. For example, the block )))(((((( despite ultimately ending at height 3, cannot be placed at the beginning. It would be better to place blocks like (, and then )((((. Therefore, the first phase of the algorithm, which we’ll call the positive phase, looks like this:

Positive Phase. Sort blocks that end above zero in descending order according to their minimum point.

Taking the bracketings proposed above, their pairs would look like this: (3, -3), (1, 0), and (3, -1). Then, sorting in descending order by minimum value gives us the order (1, 0), (3, -1), (3, -3). (Note that negative numbers decrease “upward”, i.e., -3 is less than -1).

If such an order doesn’t ensure that the graph is always above zero, we can safely say that no other order will ensure it either. I leave the exact proof that this is indeed the case for the reader to think about independently (you need to ask yourself: what would happen if a block that falls below zero by 10 was placed before a block that falls below zero by 5? Can I gain anything from this? Could I lose something if I placed them in reverse order?).

So how do we handle the order of blocks whose graphs end below zero? Intuition suggests that we first want to place blocks whose minimum is as high as possible because we have the biggest reserve thanks to blocks that “raised” the end of the graph. Can we therefore sort them by ascending minimum? The answer is… yes and no. Consider the following example with three blocks ((((, ))), and ))(. Their corresponding pairs are (4, 0), (-3, -3), and (-2, -1) respectively. If we sorted blocks that end below zero in ascending order by minimums, we would get the bracketing (((()))))(, which is obviously not valid, while the bracketing (((())())) is.

At this point, we’ll use another beautiful trick that makes the solution as simple as it was for blocks with positive endings. Notice that blocks whose graphs end below zero, when read backwards, suddenly become blocks whose graphs end above zero. And we already know how to arrange such blocks!

If a given graph ends at height A (note that A is negative), then the reflected graph will end at height -A. Moreover, its minimum value will change. In the above image, it’s easy to notice that our new minimum value must be A-B. Therefore, the negative phase of the algorithm works as follows:

Negative Phase. Change all pairs (A, B) to pairs (-A, A-B) and run the positive phase on them.

The complete algorithm thus takes the following form:

1. Check if there are as many opening brackets as closing brackets on all blocks. If not, end with failure immediately.
2. Convert all blocks into their corresponding pairs (final graph value, minimum graph value).
3. Segregate blocks into two lists, one with non-negative endings, the other with negative ones.
4. Run the first phase on non-negative blocks. If such an order creates a graph that falls below zero, end with failure.
5. Run the second phase on negative blocks. If such an order creates a graph that doesn’t fall below zero, end with success.

The solution doesn’t seem hardcore, yet no participant managed to solve it during the contest. Participants submitted many solutions that seemed correct at first glance, however, after analyzing their codes, I was able to find examples of blocks that showed their algorithm didn’t work correctly. It turned out that the second phase caused them the most problems. In their defense, I must say that in my first approach to this problem, I made the same mistake and only after some thought was I able to understand how cleverly one can deal with the second part of the blocks.

For all those interested, I cordially invite you to try solving the problem independently. The correctness of the solution can be checked here.

Thank you so much for reading until the very end! If you liked my post, have any questions or comments, do not hesitate to leave a comment or message me directly via email. Thanks and see you in the next post 🙂