Na jednych z pierwszych zajęć JFiZO został przedstawiony konstruktywny dowód na równoważność siły wyrażeń regularnych oraz deterministycznych automatów skończonych (DFA). Pokazanie, że dla każdego regexa istnieje równoważny DFA jest proste, sprawa komplikuje się w drugą stronę. Tak mi się przynajmniej na początku wydawało, ale im dłużej o tym myślałem, tym bardziej odczuwałem wrażenie, że gdzieś już ten dowód widziałem.
Tutaj można sobie zobaczyć moje notatki z JFiZO i nie tylko.
Dla ustalenia uwagi napiszę przyjmowane przeze mnie definicje (jeżeli jesteś z tym zaznajomiony, to przewiń do końca artykułu):
Definicja 1. Deterministycznym automatem skończonym (DFA) nazywamy krotkę ![]() , gdzie
, gdzie ![]() to skończony alfabet,
to skończony alfabet, ![]() to skończony zbiór stanów,
to skończony zbiór stanów, ![]() to stan początkowy,
to stan początkowy, ![]() to funkcja przejścia oraz
to funkcja przejścia oraz ![]() jest zbiorem stanów akceptujących.
jest zbiorem stanów akceptujących.
Definicja 2. ![]() nazywamy wyrażeniem regularnym oraz
nazywamy wyrażeniem regularnym oraz ![]() językiem, które wyraża to wyrażenie, gdy:
językiem, które wyraża to wyrażenie, gdy:
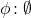 oraz
oraz 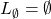 ,
,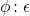 oraz
oraz 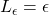 ,
,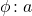 , gdzie
, gdzie 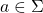 ,
,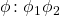 , gdzie
, gdzie 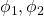 to wyrażenia regularne, wtedy
to wyrażenia regularne, wtedy 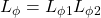 (chodzi tu o konkatenację),
(chodzi tu o konkatenację),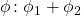 , gdzie
, gdzie 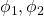 to wyrażenia regularne, wtedy
to wyrażenia regularne, wtedy 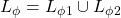 (czyli słowo pasuje do jednego lub do drugiego regexa),
(czyli słowo pasuje do jednego lub do drugiego regexa),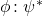 , wtedy
, wtedy 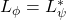 (gdzie
(gdzie 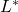 to zbiór skończonych konkatenacji słów
to zbiór skończonych konkatenacji słów
z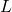 ).
).
Można zauważyć, że w definicji wyrażeń regularnych nie pojawia się kilka konstrukcji znanych z typowych regexów używanych w praktyce (często składnia się też trochę różni). Wynika to z kilku powodów, np. z tego że taka definicja jest w zupełności wystarczająca, inne są lukrem syntaktycznym (lub są niemożliwe do osiągnięcia, np. rejestry, co jest całkiem zabawne, bo takie wyrażenia przestają być regularne).
Przejdźmy do sedna, tj. do konstrukcji wyrażenia regularnego wyrażającego ten sam język, co dany DFA ![]() . W zasadzie najciekawszy dla nas będzie początek dowodu, czyli pomysł na konstrukcję szukanego wyrażenia regularnego.
. W zasadzie najciekawszy dla nas będzie początek dowodu, czyli pomysł na konstrukcję szukanego wyrażenia regularnego.
Twierdzenie. Niech ![]() będzie DFA. Wtedy istnieje wyrażenie regularne
będzie DFA. Wtedy istnieje wyrażenie regularne ![]() takie, że
takie, że ![]() , tj. zbiór słów akceptowanych przez automat jest dokładnie równy zbiorowi słów wyrażanych przez
, tj. zbiór słów akceptowanych przez automat jest dokładnie równy zbiorowi słów wyrażanych przez ![]() .
.
Dowód. Niech ![]() . Dla
. Dla ![]() skonstruujemy wyrażenie regularne
skonstruujemy wyrażenie regularne ![]() wyrażające język
wyrażające język
![]()
![]()
Uff, napis jest długi, więc postaram się go wyjaśnić bardziej opisowo. Chcemy, żeby ![]() wyrażało tylko te słowa, które ze stanu
wyrażało tylko te słowa, które ze stanu ![]() przechodzą do stanu
przechodzą do stanu ![]() , a “po drodze” odwiedzają jedynie stany o numerach mniejszych niż
, a “po drodze” odwiedzają jedynie stany o numerach mniejszych niż ![]() (nie bierzemy pod uwagę tutaj odwiedzin stanu początkowego i końcowego).
(nie bierzemy pod uwagę tutaj odwiedzin stanu początkowego i końcowego).
Powiedzmy, że dla wszystkich ![]() mamy już takie wyrażenie regularne. Wtedy
mamy już takie wyrażenie regularne. Wtedy ![]() jest szukanym przez nas wyrażeniem regularnym. Konstrukcja tych wyrażeń następuje indukcyjnie względem k:
jest szukanym przez nas wyrażeniem regularnym. Konstrukcja tych wyrażeń następuje indukcyjnie względem k:
- Dla
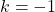 mamy
mamy 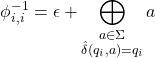 , a dla
, a dla 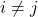 mamy
mamy 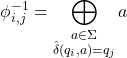 . W skrócie:
. W skrócie: 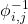 wyraża tylko te litery, którymi możemy bezpośrednio przejść z
wyraża tylko te litery, którymi możemy bezpośrednio przejść z 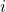 -tego stanu do
-tego stanu do 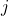 -tego.
-tego. - Załóżmy, że mamy już skonstruowane wyrażenia dla
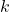 . Będziemy teraz konstruować wyrażenia dla
. Będziemy teraz konstruować wyrażenia dla 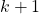 . Zanim to zrobimy, zastanówmy się jak wyglądają słowa, które są wyrażane przez
. Zanim to zrobimy, zastanówmy się jak wyglądają słowa, które są wyrażane przez 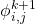 . Jeszcze raz: chcemy wyrażać słowa
. Jeszcze raz: chcemy wyrażać słowa 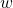 , które ze stanu
, które ze stanu 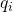 przeprowadzają nas do stanu
przeprowadzają nas do stanu 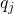 , a po drodze nie wchodzą do żadnego stanu o numerze większym niż
, a po drodze nie wchodzą do żadnego stanu o numerze większym niż 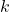 . Od razu widzimy, że na pewno słowa wyrażane przez
. Od razu widzimy, że na pewno słowa wyrażane przez 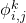 spełniają zadanie. Zostało nam zatem rozważać takie słowa, które na pewno przejdą przez stan
spełniają zadanie. Zostało nam zatem rozważać takie słowa, które na pewno przejdą przez stan 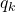 . Jak wygląda “ścieżka”, którą przesuwamy się idąc słowem
. Jak wygląda “ścieżka”, którą przesuwamy się idąc słowem 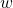 ? Zaczynamy w stanie
? Zaczynamy w stanie 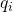 , idziemy po kolejnych literach, aż w końcu po raz pierwszy trafiamy do
, idziemy po kolejnych literach, aż w końcu po raz pierwszy trafiamy do 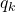 . Potem idziemy po kolejnych literach i potencjalnie kolejny raz trafiamy do
. Potem idziemy po kolejnych literach i potencjalnie kolejny raz trafiamy do 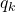 , aż w końcu ostatni raz odwiedzamy ten stan i przechodzimy bezpośrednio do
, aż w końcu ostatni raz odwiedzamy ten stan i przechodzimy bezpośrednio do 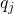 . To co teraz napiszę może wydawać się truizmem, ale jest bardzo istotne do dobrego zrozumienia konstrukcji: pomiędzy momentami odwiedzić stanu
. To co teraz napiszę może wydawać się truizmem, ale jest bardzo istotne do dobrego zrozumienia konstrukcji: pomiędzy momentami odwiedzić stanu 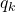 nie odwiedzamy stanu
nie odwiedzamy stanu 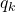 , a co za tym idzie — poruszamy się tylko po stanach o numerach mniejszych od
, a co za tym idzie — poruszamy się tylko po stanach o numerach mniejszych od 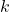 . Ale słowa, które w ten sposób przechodzą przez stany już potrafimy wyrażać! Możemy w końcu napisać:
. Ale słowa, które w ten sposób przechodzą przez stany już potrafimy wyrażać! Możemy w końcu napisać:
![]()
![]()
Okej, ale co z tym Floydem-Warshallem? Przypomnijmy algorytm:
# Początkowe wartości w tablicy dist
for i in {1..n}
for j in {1..n}
dist[i, j] = infinity
dist[i, i] = 0
# Obliczanie odległości
for k in {1..n}
for i in {1..n}
for j in {1..n}
if dist[i, j] > dist[i, k] + dist[k, j]
dist[i, j] = dist[i, k] + dist[k, j]Czy to nie wygląda podobnie? Pomysł jest w zasadzie ten sam — dynamicznie “podnosimy możliwość” przechodzenia przez kolejne wierzchołki grafu. Ucieszyło mnie takie połączenie, tym bardziej że wzięło mnie trochę z zaskoczenia. Może komuś z Was też się spodoba.
Moja implementacja algorytmu konwersji DFA do wyrażeń regularnych w OCaml.

Dziękuję za ten post i życzę powodzenia w pisaniu kolejnych!
Dziękuję 🙂
Dzięki za przypomnienie tego dowodu! To faktycznie ciekawe jak taka uporządkowana indukcja prowadzi do tak eleganckiego rozwiązania :3
A myślę, że gdyby ten dynamik zapisać w stylu top-down (czyli rekurencyjnie ze spamiętywaniem) to nawet bardziej przypominałby technikę użytą w dowodzie 😀
nice
nice